Register Automaton with Fresh Value Generation

Existing register automaton models do not allow for the generation of fresh output values. This feature is technically challenging due to the resulting non-determinism. Fresh outputs, however, are crucial in many real-world systems, e.g. servers that generate fresh identifiers, passwords or sequence numbers. That's why we extended the register automaton model with Fresh Value generation.

Formal definition Register Automaton with Fresh Value Generation

Source: [TomteFreshJournal]

In this section, we define register automata. For reasons of exposition, the notion of register automaton that we define here is a simplified version which can be easily be extended with constants and actions with multiple parameters.

We postulate a countably infinite set V of variables which contains two special variables in and out which are used to specify the data parameter of input and output actions, respectively. An atomic formula is a boolean expression of the form true, false, x=y or x≠y, with x,y∈V. A formula φ is a conjunction of atomic formulas. Let X⊆V be a set of variables. We write Φ(X) for the set of formulas with variables taken from X. A valuation for X is a function ξ:X→Z. We write Val(X) for the set of valuations for X.

Thus:

V

a countably infinite set of variables

Φ(X)

the set of formulas with variables taken from X, where a formula is a conjunction of atomic formulas of the form true, false, x=y or x≠y, with x,y∈X.

Definition 1 (Register automaton). A register automaton (RA) is a tuple R=(I,O,L,l₀,R,Γ) with

• I and O finite, disjoint sets of input and output symbols, respectively,
• L a finite set of locations and l₀ ∈ L the initial location,
• R is a function that assigns to each location l a finite set R(l)⊆V\{in,out} of registers, with R(l₀)=∅
• Γ ⊆ L × I × Φ(V) × (V ↛ V) × O × L a finite set of transitions.
• In a transition (l,i,G,U,o,l′)∈Γ, we refer to
  • l as the source location,
  • i as the input symbol,
  • G as the guard function,
  • U as the update function (a partial function),
  • o as the output symbol, and
  • l′ as the target location.
• For each transition (l,i,G,U,o,l′)∈Γ, we require that:
  • G∈Φ( R(l)∪{in,out} ) and
  • U:R(l′)→R(l)∪{in,out}.

The operational semantics of a register automaton is a Mealy machine in which the states are pairs of a location l and a valuation ξ of the registers R(l). A transition may fire for given input and output values if its guard evaluates to true. In this case, a new valuation of the registers R(l′) is computed using the update part of the transition.

For the formal definition of the operational semantics of register automata in terms of Mealy machines we refer to [TomteFreshJournal].

Example

As a first running example of a register automaton we use a FIFO-set with capacity two. A FIFO-set is a queue in which only different values can be stored, see Figure 1.

Fig. 1.FIFO-set with a capacity of 2 modeled as a register automatonThe operational semantics of register automata is defined in terms of (infinite state) Mealy machines.

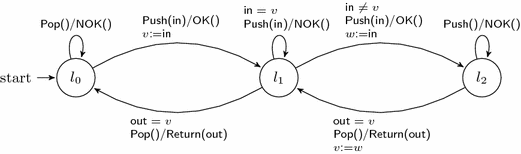
Input Push tries to insert a value in the queue, and input Pop tries to retrieve a value from the queue. The output in response to a Push is OK if the input value can be added successfully, or NOK if the input value is already in the queue or if the queue is full. The output in response to a Pop is Return, with as parameter the oldest value from the queue, or NOK if the queue is empty. We omit parameters that do not matter, and for instance write Pop() instead of Pop(in) if parameter 𝗂𝗇 does not occur in the guard and is not touched by the update.