Tag: toy
Source: http://www.wikiwand.com/en/Deterministic_finite_automaton
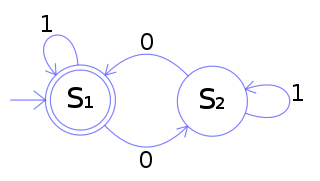
The DFA below has a binary alphabet and accepts all words that contain an even number of 0s.
M = (Q, Σ, δ, q0, F) where
| 0 | 1 | |
| S1 | S2 | S1 |
| S2 | S1 | S2 |
The state S1 represents that there has been an even number of 0s in the input so far, while S2 signifies an odd number. A 1 in the input does not change the state of the automaton. When the input ends, the state will show whether the input contained an even number of 0s or not. If the input did contain an even number of 0s, M will finish in state S1, an accepting state, so the input string will be accepted.